前回は、ニューラルネットワークの「全結合層」について簡単に説明しました。全結合層のようなニューラルネットワークの演算とセットで「活性化層」という処理がよく使われます。
今回は、その「活性化層」の説明や、そもそもなぜ必要なのかを初心者向けに解説します。
活性化層とは
実は全結合層などで計算した値をそのまま出力せず、活性化層を通すことになります。
入力→全結合層→活性化層→出力or次の全結合層
というイメージです。
活性化層は、入力された値(通常は全結合層からの出力)に何らかの数学的な操作を行い、その結果を次の層へと送ります。
なぜ活性化層が必要なのか
ここで「なぜ全結合層の出力をそのまま使ってはだめなのか」「あえて活性化層を挟む理由はなに?」という疑問が出ると思います。
その答えは、全結合層の線形な計算を活性化層によって非線形に変形できるからです。
線形とは入力と出力の関係を図示したときに、直線で表すことができる状態をいいます。逆に線形で表せないものが非線形です。
以前の全結合層の記事の例、カレーと満足度の関係で考えてみましょう。
全結合層の計算通りに行うと、カレーが一つ増えるごとに満足度は必ず4上昇します。
しかし、実際には徐々にお腹が膨れていき、満足度の上昇量は徐々に小さくなっていきます。二次関数のような曲線の関係が適切だと分かります。
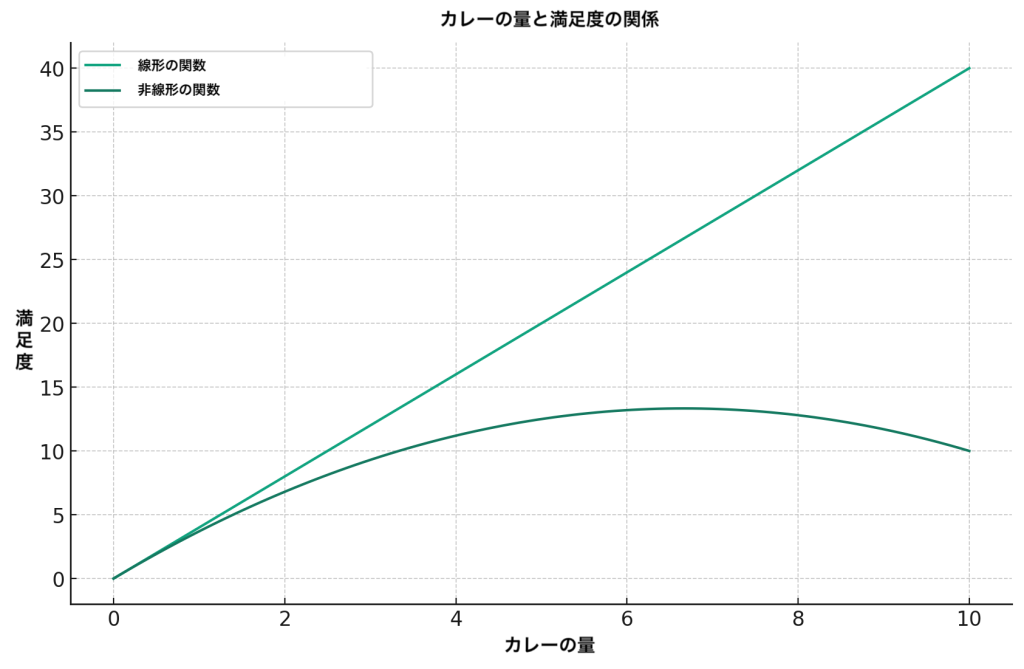
このように、線形だけでは表現できない問題が数多くあり、それに対応するために活性化層で非線形に変換するのです。
活性化関数
活性化層では活性化関数を実行することで、線形な出力を非線形へと変換しています。
代表的な活性化関数は以下の通りです。それぞれ夕食の満足度の例で説明します。
ReLU
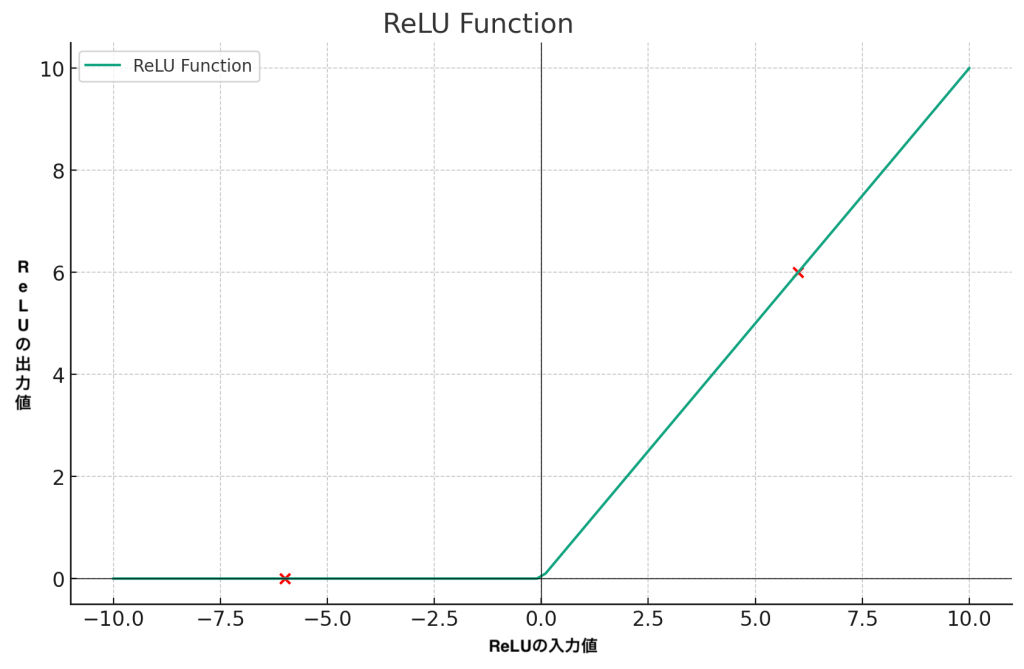
ReLUは、入力が0以下のときは0を出力し、それ以上の値はそのまま出力するという関数です。
もしアルコールが飲めないのにビールまみれの夕食会に参加するなどの場合で、全結合層の出力はマイナスになったとします。それを活性化関数のReLU関数に通すと最終的な出力は0ということになります。
もし全結合層の出力がプラス(6)だったら、ReLU関数の出力も全結合層の結果(6)をそのまま出力します。
Sigmoid
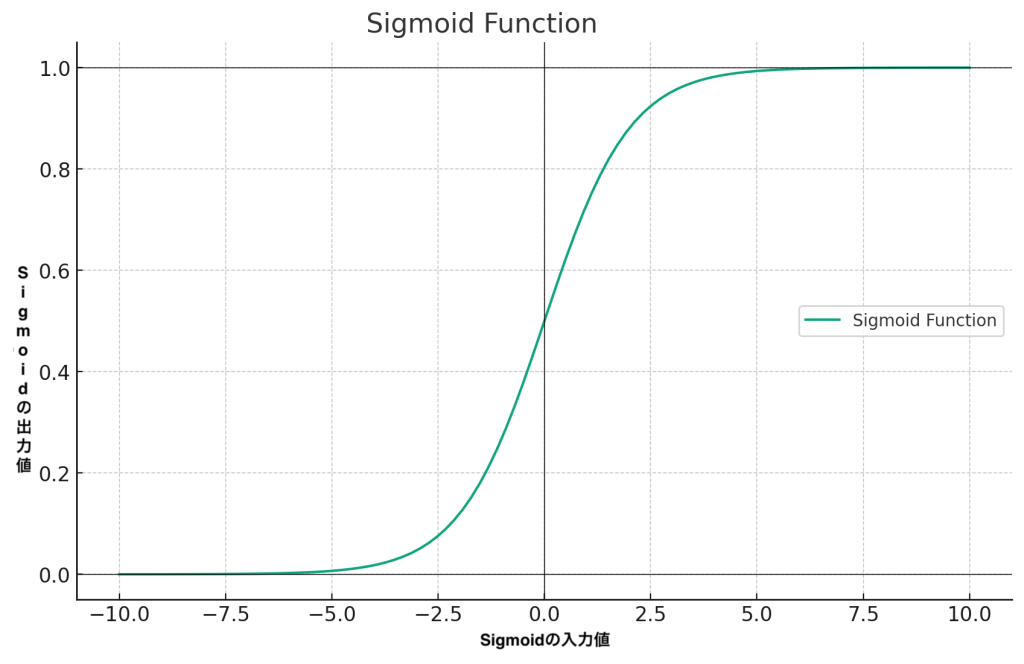
Sigmoid関数は、入力値を0から1の間の値に変換します。
この関数の特徴は、入力 x が非常に大きい負の値の場合、出力は 0 に近く、xが非常に大きい正の値の場合、出力は 1 に近くなります。
例えば、カレーを一口も食べなかった場合、満足度はほぼ 0 です。しかし、カレーを何口か食べると満足度は急激に上昇します。さらに、カレーをたくさん食べても、満足度は 1 に近づくだけで、無限には上昇しません。
これは、シグモイド関数が 0 から 1 の間の値しか取らないからです。 0 から 1 の間を取るという特性を利用して、Sigmoid関数は確率を出力する際によく利用されます。 例えば、病気にかかっている確率、明日雨が降る確率などです。
活性化層を含めたニューラルネットワークのイメージ
全結合層のような演算の出力が活性化層の入力として使われ処理されるということはイメージできたと思います。そこで、ニューラルネットワーク全体としてはどのような構造になるかを確認しておきましょう。
前回の記事で説明したモデルは以下の通りです。
入力 -> 全結合層 -> 全結合層 -> 出力
これに活性化層を導入すると以下のようになります。
入力 -> 全結合層 -> 活性化層 -> 全結合層 -> 活性化層 -> 出力
今回は出力を夕食会が成功に終わる確率として出力したいとします。すると確率を出力したいので最後の活性化層はSigmoid関数を使用するのが適切です。
それ以外の活性化層はReLU関数を使うことにします。出力層以外の活性化層ではReLU関数を使用することが多いです。なぜかというと経験上それでモデルの精度が高くなることが多いとされているからです。
以上の活性化関数を反映すると以下のようになります。
入力 -> 全結合層 -> 活性化層(ReLU) -> 全結合層 -> 活性化層(Sigmoid) -> 出力
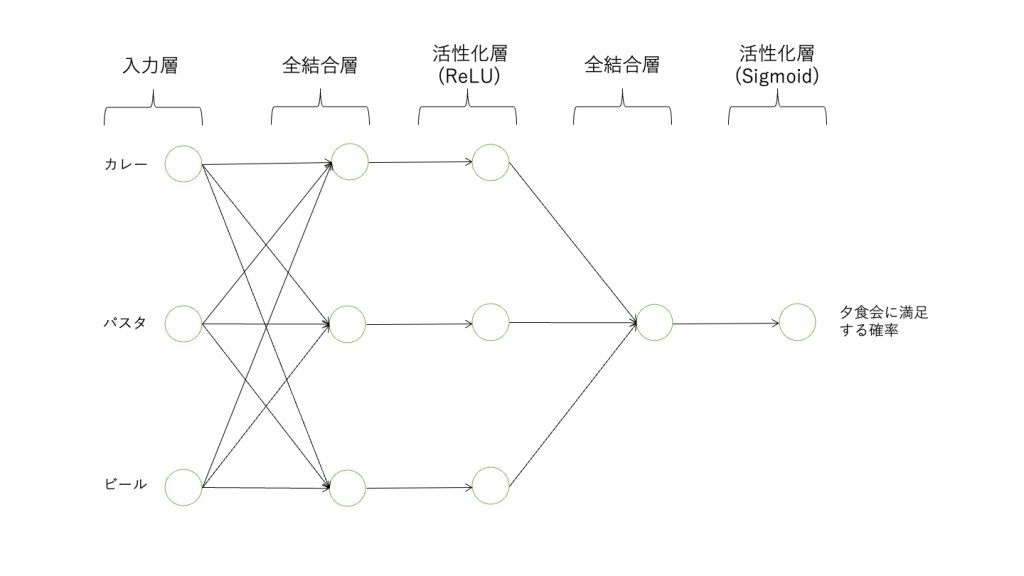
このような構造にすることで、全結合層の線形出力を活性化層で非線形の出力に変形し、最終的に出力を確率で表現することが可能となります。


