ディープラーニングで最初に学ぶ演算処理といえば全結合層だと思います。しかし、意外と計算内容の説明が行われるだけで、初心者の方が「わかった!」と腹落ちできる説明が多くないように思います。
そこで本記事では1記事丸ごと全結合層に焦点をあて、具体例をもとに分かりやすく説明しました。
もし説明で頭が混乱することがあっても、後述の具体例まで我慢して読み進めてみてください。イメージがわいて理解に役立ちます。
全結合層とは
全結合層とは、ニューラルネットワークにおけるデータを処理するための演算の一つです。全結合層の演算により、データの情報を組み合わせて新しい情報を作り出すことができます。
具体的には、入力データのリストに対して重要度(重み)を掛け算して足し合わせ、バイアスを加えます。計算式は以下の通りです。
y = Wx + b
y -> 出力ベクトル
W -> 重み行列
x -> 入力ベクトル
b -> バイアス
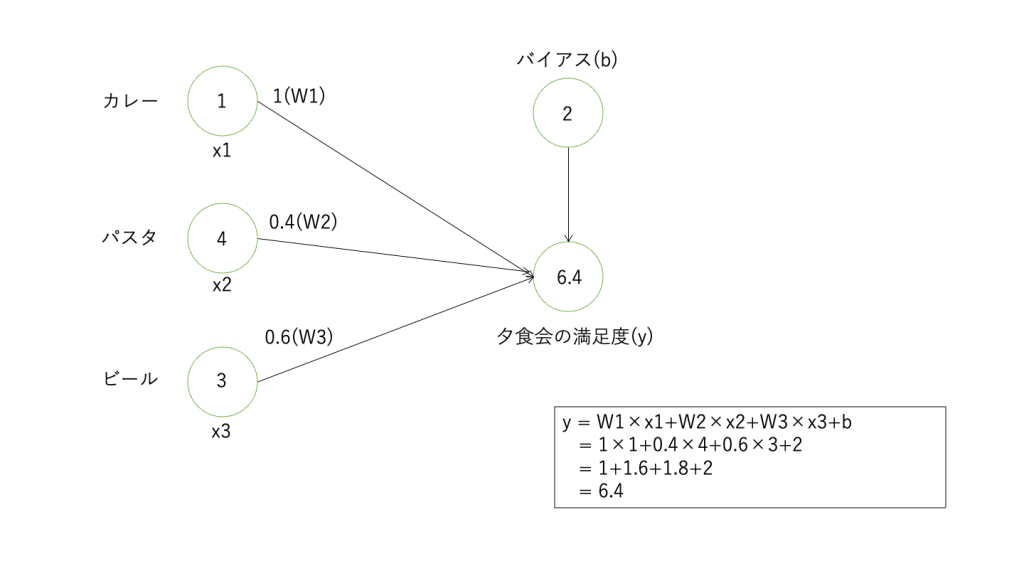
分かりづらいと思うので、具体例を出しましょう。 あなたは夕食に呼ばれました。テーブルの上には料理が3品並んでいます。
料理が入力ベクトル(x1 ,x2, x3)であり、それぞれの料理に対するあなたの好みが重み(W1, W2, W3)を表します。そして、あなたが各料理から得られる満足度は、料理(入力ベクトル)とあなたの好み(重み)の掛け算の結果となります。それら全ての料理から得られる満足度を足し合わせたもの(y)が全結合層の計算の結果となります。
バイアス(b)は、食事の満足度を一律に増減させる要素と考えることができます。例えば、料理が何もない場合でも、あなたが前日から楽しみにしていたり、周囲の雰囲気が良かったりすると、それだけで満足感があるかもしれません。そのような一律の増減を表すのがバイアスです。
全結合層の計算(複数出力)
全結合層の計算結果はリストで出力することが一般的です。出力が複数になると、出力に対応する重みをそれぞれ用意する必要があります。
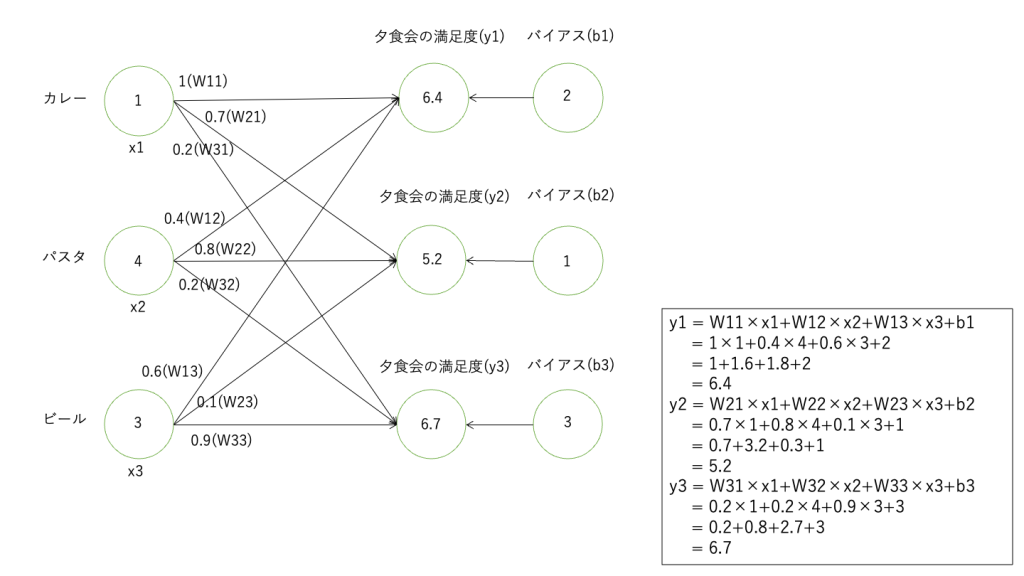
また食事の例で考えてみましょう。先ほどは出力としてあなたの満足度を計算しましたが、夕食を3人で食べ、3人それぞれの満足度を出力したいとします。
テーブルの上の料理、入力ベクトル(x)は3人とも同じです。しかし、3人それぞれ好みやがあるので、重み(W)は異なります。夕食の場に対する印象も人によって異なるのでバイアス(b)もそれぞれ異なります。
1人目の満足度をy1とすると、料理x1に対するその人の好みをw11、バイアスをb1と定義して計算します。
2人目の場合も満足度をy2とすると、料理x1に対するその人の好みをw21、その人のバイアスb2とします。
入力データは共通で、重みとバイアスは個別に存在するということがポイントです。
ディープニューラルネットワーク
全結合層のような層計算を縦に積み上げてより複雑な計算が可能なモデルを作成することができます。特に多くの層を積み上げた深いモデルをディープニューラルネットワークといいます。
2つの全結合層を縦に積み上げたモデルを考えてみましょう。一つの全結合層の計算結果が次の全結合層の入力値となります。それぞれの全結合層の計算方法は変わらないのですが、おそらく分からないのは「なぜ全結合層を縦に積み上げる意味があるの?」ということだと思います。
そこで、また夕食の例で説明しましょう。
前回では3人の夕食の満足度を算出しました。そこから夕食会全体の成功度を出したいとします。
すると、入力値は3人の夕食の満足度、重みは誰の満足度を重視するか、バイアスは3人の満足度とは別の要素(夕食会を開催すること自体への満足度など)を表し、出力結果が夕食会全体の成功度となります。
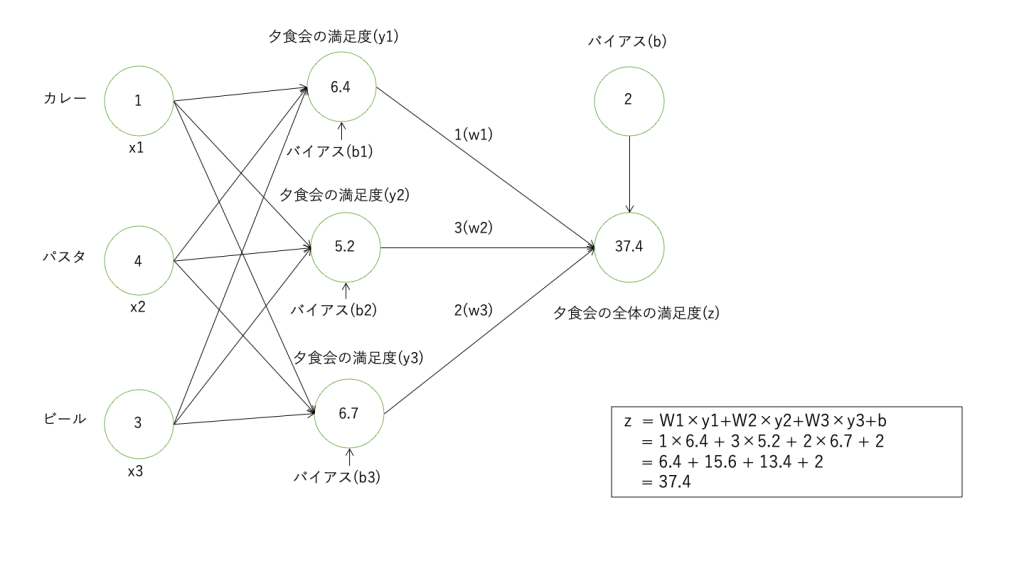
このように全結合層の出力を次の全結合層の入力値とすることで層を重ねることができ、料理から夕食の満足度を算出するという複雑な計算を行うことができます。
この記事を通して、全結合層の基本的な概念と計算プロセスについて説明しました。
全結合層はニューラルネットワークの演算処理の中で最も基本となるものなので、ここでしっかり理解しておきましょう。


